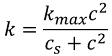Numerical Integration Formulas

Here are the M-files to implement composite trapezoidal rule for equally spaced data and unequally spaced data. 

Composite Trapezoidal Rule (Equally Spaced Data) M-file

function I = trap(func,a,b,n,varargin)

% trap: composite trapezoidal rule quadrature

% I = trap(func,a,b,n,pl,p2,...):

% composite trapezoidal rule

% input:

% func = name of function to be integrated

% a, b = integration limits

% n = number of segments (default = 100)

% pl,p2,... = additional parameters used by func

% output:

% I = integral estimate

if nargin<3,error('at least 3 input arguments required'),end

if ~(b>a),error('upper bound must be greater than lower'),end

if nargin<4|isempty(n),n=100;end

x = a; h = (b - a)/n;

s=func(a,varargin{:});

for i = 1 : n-1

x = x + h;

s = s + 2*func(x,varargin{:});

end

s = s + func(b,varargin{:});

I = (b - a) * s/(2*n);

Composite Trapezoidal Rule (Unequally Spaced Data) M-file

function I = trapuneq(x,y)

% trapuneq: unequal spaced trapezoidal rule quadrature

% I = trapuneq(x,y):

% Applies the trapezoidal rule to determine the integral

% for n data points (x, y) where x and y must be of the

% same length and x must be monotonically ascending

% input:

% x = vector of independent variables

% y = vector of dependent variables

% output:

% I = integral estimate

if nargin<2,error('at least 2 input arguments required'),end

if any(diff(x)<0),error('x not monotonically ascending'),end

n = length(x);

if length(y)~=n,error('x and y must be same length'); end

s = 0;

for k = 1:n-1

s = s + (x(k+l)-x(k))*(y(k)+y(k+l))/2;

end

I = s;

Numerical Integration Formulas

Problem 19.13.

The total mass of a variable density rod is given by 

where m = mass, ρ(x) = density, A_c(x) = cross-sectional area, x = distance along the rod, and L = total length of rod. The following data have been measured for a 20-m (L) length rod. Determine the mass in grams to the best possible accuracy. 

Solution:

First, be aware of the units. Convert the unit for distance into cm to ensure the calculation is dimensionally homogenous. Also, compute the product of density and cross-sectional area of the rod. 

To attain best possible accuracy for the integral, we can apply combination of trapezoidal rule (1st segment), Simpson's 1/3 rule (2nd & 3rd segments) and Simpson's 3/8 rule (last three segments). 

Numerical Integration Formulas

Problem 19.5.

The function f(x) = e^-x can be used to generate the following table of unequally spaced data: 

Evaluate the integral from a = 0 to b = 1.2 using (a) analytical means, (b) the trapezoidal rule, and (c) a combination of the trapezoidal and Simpson's rules wherever possible to attain the highest accuracy. For (b) and (c), compute the true percent relative error. 

Solution:

(a) The analytical solution can be evaluated as

(b) Apply trapezoidal rule to each segment and sum the results

(c) Apply trapezoidal rule to the first segment (h = 0.1), Simpson's 3/8 rule to the next three segments (h = 0.2), and Simpson's 1/3 rule to the last two segments (h = 0.25). Then, sum the results

Polynomial Interpolation: Inverse Interpolation

Problem 17.9.

Employ inverse interpolation to determine the value of x that corresponds to f(x) = 0.93 for the following tabulated data: 

Note that the values in the table were generated with the function f(x) = x²/(1+x²).

(a) Determine the correct value analytically. 

(b) Use quadratic interpolation and the quadratic formula to determine the value numerically. 

(c) Use cubic interpolation and bisection to determine the value numerically. 

Solution:

(a) Using the function available, manipulate it to determine corresponding x value:

(b) A quadratic interpolating polynomial can be fit to the last three points: (3, 0.9), (4, 0.941176), and (5, 0.961538) using polyfit function:

>> format long

>> x = [3 4 5];

>> fx = [0.9 0.941176 0.961538];

>> a = polyfit(x,fx,2)

a =

  -0.010407000000000   0.114024999999999   0.651588000000002

Thus, the best-fit parabola that passes through the last three points is f₂(x) = -0.010407x² + 0.114025x + 0.651588. 

We must therefore find the root of 

0.93 = -0.010407x² + 0.114025x + 0.651588

or

0 = -0.010407x² + 0.114025x - 0.278412

The quadratic formula can be used to calculate:

Thus, the second root, 3.67295, is a good estimate of the true value. 

(c) A cubic interpolating polynomial can be fit to the last four points: (2, 0.8), (3, 0.9), (4, 0.941176), and (5, 0.961538) using polyfit function:

>> format long

>> x = [2 3 4 5];

>> fx = [0.8 0.9 0.941176 0.961538];

>> a = polyfit(x,fx,3)

a =

   0.006335000000000  -0.086427000000002   0.411770000000007   0.271487999999994

Thus, the best-fit cubic that passes through the last four points is f₃(x) = 0.006335x³ - 0.086427x² + 0.41177x + 0.271488. 

We must therefore find the root of 

0.93 = 0.006335x³ - 0.086427x² + 0.41177x + 0.271488

or

0 = 0.006335x³ - 0.086427x² + 0.41177x - 0.658512

Bisection method (bisect.m) can be employed to find the root of this polynomial. Using initial guesses of x_l = 3 and x_u = 4 (that bracket the root), a value of 3.61884 is obtained.

>> fx = @(x) 0.006335*x^3 - 0.086427*x^2 + 0.41177*x - 0.658512;

>> [root,fx,ea,iter]=bisect(fx,3,4)

root =

   3.618841171264648

fx =

     1.082876788238707e-08

ea =

     5.270606093347705e-05

iter =

    19

Polynomial Interpolation

Problem 17.5.

Given the data

Calculate f(4) using Newton's interpolating polynomials of order 1 through 4. Choose your base points to attain good accuracy. That is, the points should be centered around and as close as possible to the unknown. What do your results indicate regarding the order of the polynomial used to generate the data in the table? 

Solution:

The points can be ordered so that they are close to and centered around the unknown. A divided-difference table can then be developed as:

Note that the fact that the fourth divided difference is zero means that the data was generated with a third-order polynomial.

Polynomial Interpolation

Problem 17.4.

Given the data 

(a) Calculate f(3.4) using Newton's interpolating polynomials of order 1 through 3. Choose the sequence of the points for your estimates to attain the best possible accuracy. That is, the points should be centered around and as close as possible to the unknown. 

(b) Repeat (a) but use the Lagrange polynomial. 

Solution:

(a) Newton's interpolating polynomial. Ordering of points:

Note that based purely on the distance from the unknown (nearer to 3.4), the fourth point would be (2,5). However, because it provides better balance and is located only a little bit farther from the unknown, the point at (5,0) is chosen.

Set up divided difference table to ease the evaluation of each order of polynomial interpolation. 

First divided differences:

Second divided differences:

Third divided difference:

Thus, the divided difference table is

First order (linear) interpolation:

Second order (quadratic) interpolation:

Third order (cubic) interpolation:

(b) Lagrange interpolating polynomial.

First order interpolation:

Second order interpolation:

Third order interpolation:

Polynomial Interpolation

Here are the M-files to implement Newton interpolation and Lagrange interpolation.

Newton Interpolation M-file

function yint = Newtint(x,y,xx)
% Newtint: Newton interpolating polynomial
% yint = Newtint(x,y,xx): Uses an (n - 1)-order Newton
% interpolating polynomial based on n data points (x, y)
% to determine a value of the dependent variable (yint)
% at a given value of the independent variable, xx.
% input:
% x = independent variable
% y = dependent variable
% xx = value of independent variable at which
% interpolation is calculated
% output:
% yint = interpolated value of dependent variable

% compute the finite divided differences in the form of a
% difference table
n = length(x);
if length(y)~=n, error('x and y must be same length'); end
b = zeros(n,n);
% assign dependent variables to the first column of b.
b(:,1) = y(:); % the (:) ensures that y is a column vector.
for j = 2:n
for i = 1:n-j+1
b(i,j) = (b(i+1,j-1)-b(i,j-1))/(x(i+j-1)-x(i));
end
end
% use the finite divided differences to interpolate
xt = 1;
yint = b(1,1);
for j = 1:n-1
xt = xt*(xx-x(j));
yint = yint+b(1,j+1)*xt;
end

Lagrange Interpolation M-file

% Lagrange interpolating polynomial based on n data points

% to determine a value of the dependent variable (yint) at

% a given value of the independent variable, xx.

% input:

% x = independent variable

% y = dependent variable

% xx = value of independent variable at which the

% interpolation is calculated

% output:

% yint = interpolated value of dependent variable

n = length(x);

if length(y)~=n, error('x and y must be same length'); end

s = 0;

for i = 1:n

product = y(i);

for j = 1:n

if i ~= j

product = product*(xx-x(j))/(x(i)-x(j));

end

end

s = s+product;

end

yint = s;

Nonlinear Regression

Problem 15.11.

The following model is used to represent the effect of solar radiation on the photosynthesis rate of aquatic plants:

where P = the photosynthesis rate (mg m^-3d^-1), P_m = the maximum photosynthesis rate (mg m^-3d^-1), I = solar radiation (µE m^-2s^-1), and I_sat = optimal solar radiation (µE m^-2s^-1). Use nonlinear regression to evaluate P_m and I_sat based on the following data:

Solution:

First, a M-file function must be created to compute the sum of squares: 

function f = fSSR(a,Im,Pm)

Pp = a(1)*Im/a(2).*exp(-Im/a(2)+1);

% a(1) = Pm, a(2) = Isat

f = sum((Pm-Pp).^2);

In command mode, the data can be entered as:

>> I = [50 80 130 200 250 350 450 550 700];

>> P = [99 177 202 248 229 219 173 142 72];

Employ initial guesses of 200 for the coefficients. The minimization of the function is then implemented by:

>> a = fminsearch(@fSSR, [200, 200], [], I, P)

a =

  238.7124  221.8239

The best-fit model is therefore

The fit along with the data can be displayed graphically as:

>> Ip = linspace(min(I),max(I));

>> Pp = a(1)*Ip/a(2).*exp(-Ip/a(2)+1);

>> plot(I,P,'o',Ip,Pp)

>> xlabel('I'),ylabel('P')

>> title('Effect of solar radiation on photosynthesis rate')

General Linear Least-Squares Regression

Problem 15.10.

Three disease-carrying organisms decay exponentially in a seawater according to the following model:

p(t) = Ae^-1.5t + Be^-0.3t + Ce^-0.05t 

Use general linear least-squares to estimate the initial concentration of each organism (A, B and C) given the following measurements:

Solution:

Firstly, note that the given model is actually a multiple linear function, where e^-1.5t, e^-0.3t and e^-0.05t are x₁, x₂ and x₃ respectively. And there is no intercept. Let's solve the problem using MATLAB!

The data can be entered as column vectors and the [Z] matrix can be set up as below:

>> t = [0.5 1 2 3 4 5 6 7 9]';

>> p = [6 4.4 3.2 2.7 2 1.9 1.7 1.4 1.1]';

>> x1 = exp(-1.5*t); x2 = exp(-0.3*t); x3 = exp(-0.05*t);

>> Z = [x1 x2 x3]

Z =

    0.4724    0.8607    0.9753

    0.2231    0.7408    0.9512

    0.0498    0.5488    0.9048

    0.0111    0.4066    0.8607

    0.0025    0.3012    0.8187

    0.0006    0.2231    0.7788

    0.0001    0.1653    0.7408

    0.0000    0.1225    0.7047

    0.0000    0.0672    0.6376

Then, the coefficients can be generated using Eq.(15.10) in textbook:

>> a = (Z'*Z)\(Z'*p)

a =

    4.1375 = A

    2.8959 = B

    1.5349 = C

Thus, the least-squares fit is p(t) = 4.1375e^-1.5t + 2.8959e^-0.3t + 1.5349e^-0.05t .

Best-fit line and the data can be plotted as

>> pp = Z*a;

>> plot(t,p,'bo',t,pp,'k-')

>> xlabel('t'),ylabel('p'),title('Decay Exponential Model')

General Linear Least-Squares Regression

Here are the M-files to implement quadratic (second-order polynomial) regression, multiple linear regression and general linear least-squares regression.

Quadratic Regression M-file

function [a,r2,syx] = polyregr(order,x,y)

% polyregr: least-squares regression curve fitting (quadratic)

%   [a, r2] = polyregr(x,y): Least squares fit of curve line to data by solving the normal equations

% input:

%   x = independent variable

%   y = dependent variable

% output:

%   a = vector of coefficients->> a(1):intercept,a(2):slope x,a(3):slope x2

%   r2 = coefficient of determination

%   syx = standard error of estimate

n = length(x);

if length(y)~=n, error('x and y must be same length'); end

% error checking to have complete quantity of data point

x = x(:); y = y(:); % convert to column vectors

sx = sum(x); sy = sum(y);

sx2 = sum(x.^2); sxy = sum(x.*y);

sx3 = sum(x.^3); sx4 = sum(x.^4); sx2y = sum(x.*x.*y);

matrix = [n sx sx2; sx sx2 sx3; sx2 sx3 sx4];

right = [sy sxy sx2y]';

a = matrix \ right;

% to calculate error statistics

Sr = sum((y-a(1)-(a(2)*x)-(a(3)*x.^2)).^2);

St = sum((y-(sy/n)).^2);

r2 = (St-Sr)/St;

syx = sqrt(Sr/(length(x)-length(a)));

% create plot of data and best fit line

xp = min(x):0.1:max(x);

yp = zeros(1,length(xp));

    for k = 1:length(yp) 

        for l = 0:order

            yp(k) = yp(k) + a(l+1)*(xp(k))^l;

        end

    end

plot(x,y,'o',xp,yp),xlabel('T (K)'),ylabel('cp (J mol-1 K-1')

grid on

Multiple Linear Regression M-file

function [a,Sr,r2,syx] = multilinear(x1,x2,y)

% multilinear: multiple linear regression curve fitting

% input:

%   x1 = independent variable 1

%   x2 = indepencent variable 2

%   y  = dependent variable (function of x1 and x2)

% output:

%   a   = vector of coefficient->> a(1)= intercept,a(2)= slope x1,a(3)= slope x2

%   Sr  = sum of square of residuals

%   r2  = coefficient of determination

%   syx = standard error of estimate

n = length(y);

if length(x1)~=n, error('x1 and y must be same length'); end

if length(x2)~=n, error('x2 and y must be same length'); end

x1 = x1(:); x2 = x2(:); y = y(:); % convert to column vectors

sx1 = sum(x1);sx2 = sum(x2);sy = sum(y);sx1x2 = sum(x1.*x2);

sx1y = sum(x1.*y); sx2y = sum(x2.*y);

sx1sq = sum(x1.*x1); sx2sq = sum(x2.*x2);

%calculate for coefficients [a]

A = [n sx1 sx2;sx1 sx1sq sx1x2;sx2 sx1x2 sx2sq];

b = [sy;sx1y;sx2y];

a = A\b;

%calculate for Sr

yp = a(1)+a(2)*x1+a(3)*x2;

Sr = sum((y-yp).^2);

%calculate for syx

syx = sqrt(Sr/(n-length(a)));

%calculate for r2

r2 = 1-(Sr/sum((y-mean(y)).^2));

end

General Linear Regression M-file

function [a, r2, syx] = genlinreg(x1,x2,y)

% genlinreg: general linear least-squares regression model 

%   [a, r2, syx] = genlinreg(x,y): Least squares fit of line to data by solving the normal equations

% input:

%   x1 = independent variable 1

%   x2 = independent variable 2 = zeros(size(x1)) for polynomial regression

%   y  = dependent variable

% output:

%   a   = vector of coefficients->> a(1):intercept,a(2):slope for x1/x,a(2):slope of x2/x^2

%   r2  = coefficient of determination

%   syx = standard error of estimate

n = length(y);

if length(x1)~=n, error('x1 and y must be same length'); end

if length(x2)~=n, error('x2 and y must be same length'); end

x1 = x1(:); x2 = x2(:); y = y(:); % convert to column vectors

if x2 == zeros(size(x1))

    Z = [ones(size(x1)) x1 x1.^2]; 

else 

    Z = [ones(size(y)) x1 x2];

end 

a = (Z'*Z)\(Z'*y); %solve for the unknown coefficients by utilizing backslash operator 

% calculate for coefficient of determination

Sr = sum((y-Z*a).^2);

St = sum((y-mean(y)).^2);

r2 = 1-Sr/St;

% calculate for standard error of estimate

syx = sqrt(Sr/(n-length(a)));

end

General Linear Least-Squares

Problem 15.6.

Use multiple linear regression to derive a predictive equation for dissolved oxygen concentration as a function of temperature and chloride based on the data from Table P15.5. Use the equation to estimate the concentration of dissolved oxygen for a chloride concentration of 15 g/L at T = 12 °C. Note that the true value is 9.09 mg/L. Compute the percent relative error for your prediction. Explain possible causes for the discrepancy. 

Table P15.5 Dissolved oxygen concentration in water as a function of temperature (°C) and chloride concentration (g/L)

Solution:

The multiple linear regression to evaluate is 

*y is dissolved oxygen concentration (mg/L).

The [Z] and y matrices can be set up using MATLAB commands:

>> %enter the data T, c & y to be fit

>> T = [0 5 10 15 20 25 30 0 5 10 15 20 25 30 0 5 10 15 20 25 30]';

>> c = [0 0 0 0 0 0 0 10 10 10 10 10 10 10 20 20 20 20 20 20 20]';

>> y = [14.6 12.8 11.3 10.1 9.09 8.26 7.56 12.9 11.3 10.1 9.03 8.17 7.46 6.85 11.4 10.3 8.96 8.08 7.35 6.73 6.20]';

>> %create the [Z] matrix

>> Z = [ones(size(T)) T c];

>> %solve for the coefficients of the least-squares fit

>> a = (Z'*Z)\(Z'*y)

a =

  13.522142857142857

  -0.201238095238095

  -0.104928571428572

Thus, the best fit multiple regression model is

We can evaluate the prediction at T = 12°C and c = 15 g/L and evaluate the percent relative error as

>> yp = a(1)+a(2)*12+a(3)*15

yp =

   9.533357142857142

>> ea = abs((9.09-yp)/9.09)*100

ea =

   4.877416313059866

Thus, the error is considerable. This can be seen even better by generating predictions for all the data and then generating a plot of the predictions versus the measured values. A one-to-one line is included to show how the predictions diverge from a perfect fit.

>> yp = a(1)+a(2).*T+a(3).*c;

>> ymin = min(y);ymax = max(y);

>> dy = (ymax - ymin)/100;

>> ymod = [ymin:dy:ymax];

>> plot(y,yp,'ko',ymod,ymod,'k-')

>> axis square,title('Plot of predicted vs measured values of dissolved oxygen concentration')

>> legend('model prediction','1:1 line','Location','Northwest')

>> xlabel('y measured'),ylabel('y predicted')

The cause for the discrepancy is because the dependence of oxygen concentration on the unknowns is significantly nonlinear. It should be noted that this is particularly the case for the dependency on temperature.

Gauss Elimination

Here are the M-files to implement naive Gauss Elimination and Gauss Elimination with partial pivoting.

Naive Gauss Elimination M-file

function x = GaussNaive(A,b)

% GaussNaive: naive Gauss elimination

%   x = GaussNaive(A,b): Gauss elimination without pivoting.

% input:

%   A = coefficient matrix

%   b = right hand side vector

% output:

%   x = solution vector

[m,n] = size(A);

% m = no of rows, n = no of columns, size of matrix A is m x n

if m~=n, error('Matrix A must be square'); end

% if m not equal to n, error message is displayed as 'Matrix A must be square'

nb = n+1;

% no of columns for augmented matrix = no of columns of the matrix A + 1 column for the vector B

Aug = [A b];

% Coefficient matrix A and right-hand-side vector b are combined in an augmented matrix

% forward elimination

for k = 1:n-1

    % k represents column 1 to (n-1)th column

  for i = k+1:n

      % i represents row 2 to nth row

    factor = Aug(i,k)/Aug(k,k);

    % to compute the factor in order to obtain the upper triangular matrix

    Aug(i,k:nb) = Aug(i,k:nb)-factor*Aug(k,k:nb);

    % to compute the new equations until transform the matrix into upper triangular form

    % the new ith row kth column elements is equal to the old ith row kth column elements 

    % minus the multiplication of factor and kth row kth column elements 

    % since using augmented matrix, need to use nb (n+1) because of additional 1 column vector b

  end

end

% back substitution

x = zeros(n,1);

% solution vector x is a matrix of zero coefficients of n x 1 dimension

% n =  no of equations

x(n) = Aug(n,nb)/Aug(n,n);

% to calculate the last unknown x in nth equation

% by dividing the constant b in last equation with the coefficient of x(n)

% formula is same as Eq (9.12) in textbook

for i = n-1:-1:1

    % i represents no of equations (n) minus 1 with increment of -1 until 1

  x(i) = (Aug(i,nb)-Aug(i,i+1:n)*x(i+1:n))/Aug(i,i);

  % to calculate the remaining unknown x's in (n-1)th equation and so on until the first equation

  % formula is same as Eq (9.13) in textbook

end

Gauss Elimination with Partial Pivoting M-file

function x = GaussPivot(A,b)

% GaussPivot: Gauss elimination pivoting

%   x = GaussPivot(A,b): Gauss elimination with pivoting.

% input:

%   A = coefficient matrix

%   b = right hand side vector

% output:

%   x = solution vector

[m,n]=size(A);

% m = no of rows, n = no of columns,size of matrix A is m x n 

if m~=n, error('Matrix A must be square'); end

% if m not equal to n, error message will be displayed as 'Matrix A must be square'

nb=n+1;

% no of columns of augmented matrix = no of columns of matrix A + 1 column of vector b 

Aug=[A b];

% forward elimination

for k = 1:n-1

    % k represents column 1 to (n-1)th column

  % partial pivoting

  [big,i]=max(abs(Aug(k:n,k)));

  % to determine the coefficient with the largest absolute value in the column below the pivot element

  % big = largest element

  % i = index corresponding to the largest element (no of row)

  ipr=i+k-1;

  % new row (with largest element below the pivot element)= old row (with pivot element)+ k - 1

  if ipr~=k

      % if new row doesn't equal to k (row with largest element isn't row 1)

    Aug([k,ipr],:)=Aug([ipr,k],:);

    % to switch the row with largest pivot element to the first row

  end

  for i = k+1:n

      % i represents row 2 to nth row

    factor=Aug(i,k)/Aug(k,k);

    % to compute the factor in order to obtain the upper triangular matrix

    Aug(i,k:nb)=Aug(i,k:nb)-factor*Aug(k,k:nb);

    % to compute the new equations until transform the matrix into upper triangular form

    % the new ith row kth column elements is equal to the old ith row kth column elements 

    % minus the multiplication of factor and kth row kth column elements 

    % since using augmented matrix, need to use nb (n+1) because of additional 1 column vector b

  end

end

% back substitution

x=zeros(n,1);

% solution vector x is a matrix of zero coefficients of n x 1 dimension

% n =  no of equations

x(n)=Aug(n,nb)/Aug(n,n);

% to calculate the last unknown x in nth equation

% by dividing the constant b in last equation with the coefficient of x(n)

% formula is same as Eq (9.12) in textbook

for i = n-1:-1:1

    % i represents no of equations (n) minus 1 with increment of -1 until 1

  x(i)=(Aug(i,nb)-Aug(i,i+1:n)*x(i+1:n))/Aug(i,i);

  % to calculate the remaining unknown x's in (n-1)th equation and so on until the first equation

  % formula is same as Eq (9.13) in textbook

end

Linear Least-Squares Regression

Problem 14.14.

An investigator has reported the data tabulated below for an experiment to determine the growth rate of bacteria k (per d) as a function of oxygen concentration c (mg/L). It is known that such data can be modeled by the following equation: 

 Eq.(14.14(a))

where c_s and k_max are parameters. Use a transformation to linearize this equation. Then use linear regression to estimate c_s and k_max and predict the growth rate at c = 2 mg/L.

Solution:

Equation (14.14(a)), which is in the format of saturation-growth-rate model can be linearized by inverting it to give:

Thus, a plot of 1/k (y) versus 1/c² (x) will yield a straight line with a slope of c_s/k_max and an intercept of 1/k_max. The data can be set up in tabular form and the necessary sums computed as in table below.

The means can be computed as:

The slope and intercept can then be calculated with Eqs (14.15) and (14.16) as in textbook.

The least-squares fit of the transformed data is 1/k = 0.09666 + 0.20201(1/c²).

The model coefficients can then be calculated as:

k_max = 1/0.09666 = 10.34554

c_s = 0.20201 x 10.34554 = 2.0899

The growth rate at c = 2 mg/L can be predicted as:

1/k = 0.09666 + 0.20201(1/4) = 0.1471625

k = 6.7952 per day

*The linregr M-file can also be used to determine the least-squares fit:

>> format long

>> c = [0.5 0.8 1.5 2.5 4];

>> k = [1.1 2.5 5.3 7.6 8.9];

>> [a,r2,syx] = linregr(1./c.^2,1./k)

a =

   0.202005196520525   0.096665700618091

r2 =

   0.999569288346182

syx =

   0.007995513530533

The model coefficients can then be calculated as:

>> kmax = 1/a(2)

kmax =

  10.344930969370603

>> cs = kmax*a(1)

cs =

   2.089729813458969

Linear Least-Squares Regression

Here is an M-file to implement linear regression. 

Linear Regression M-file

function [a,r2,syx] = linregr(x,y)

% linregr: linear regression curve fitting

%   [a, r2] = linregr(x,y): Least squares fit of straight line to data by solving the normal equations

% input:

%   x = independent variable

%   y = dependent variable

% output:

%   a = vector of slope, a(1), and intercept, a(2)

%   r2 = coefficient of determination

%   syx = standard error of estimate

n = length(x); % show number of data

if length(y)~=n, error('x and y must be same length'); end

% error checking to have complete number of data points

x = x(:); y = y(:); % convert to column vectors

sx = sum(x); sy = sum(y);

sx2 = sum(x.*x); sxy = sum(x.*y); sy2 = sum(y.*y);

a(1) = (n*sxy-sx*sy)/(n*sx2-sx^2); % a(1) = slope

a(2) = sy/n-a(1)*sx/n; % a(2) = intercept

r2 = ((n*sxy-sx*sy)/sqrt(n*sx2-sx^2)/sqrt(n*sy2-sy^2))^2;

Sr = sum((y-a(2)-a(1)*x).^2);

St = sum((y-mean(y)).^2);

syx = sqrt(Sr/(n-2)); 

% create plot of data and best fit line

xp = linspace(min(x),max(x),2);

yp = a(1)*xp+a(2);

% best fit line equation

plot(x,y,'o',xp,yp),xlabel('x'),ylabel('y')

% to generate plot of x vs y with circle marker and plot for best fit line

grid on

Linear Least-Squares Regression

Problem 14.9.

The concentration of E.coli bacteria in a swimming area is monitored after a storm:

The time is measured in hours following the end of the storm and the unit CFU is a "colony forming unit". Use this data to estimate (a) the concentration at the end of the storm (t = 0) and (b) the time at which the concentration will reach 200 CFU/100 mL. Note that your choice of model should be consistent with the fact that negative concentrations are impossible and that the bacteria concentration always decreases with time. 

Solution:

Based on the clues provided (underlined), we can expect the model best describes the given data should be exponential model.

The above equation can be linearized by taking its natural logarithm to yield:

Thus, a plot of ln c (y) versus t (x) will yield a straight line with a slope of β and an intercept of ln α.

The data can be set up in tabular form and the necessary sums computed as in table follow.

The mean can be computed as: 

The slope and intercept can then be calculated with Eq.(14.15) and (14.16) as in textbook:

Hence, the least-squares fit of transformed data is ln c = 7.5936 - 0.053506t.

The coefficients of the exponential model are determined as α = exp(7.5936) = 1985.44 and β = -0.053506. Thus, the least-squares exponential fit is c = 1985.44e^-0.053506t. Using this exponential fit, we can solve for:

(a) When t = 0: c = 1985.44 CFU/100 mL. 

(b) When c = 200: t = 42.898 hours. 

Figure below showed the exponential model fit along with the data. 

*MATLAB commands to generate the plot:

>> t = [4 8 12 16 20 24];

>> c = [1600 1320 1000 890 650 560];

>> tp = linspace(min(t),max(t));

>> cp = 1985.44*exp(-0.053506*tp);

>> plot(t,c,'o',tp,cp),grid,xlabel('t (hr)'),ylabel('c (CPU/100 mL)')