Problem 14.14.
An investigator has reported the data tabulated below for an experiment to determine the growth rate of bacteria k (per d) as a function of oxygen concentration c (mg/L). It is known that such data can be modeled by the following equation:
Eq.(14.14(a))
where cs and kmax are parameters. Use a transformation to linearize this equation. Then use linear regression to estimate cs and kmax and predict the growth rate at c = 2 mg/L.
Solution:
Equation (14.14(a)), which is in the format of saturation-growth-rate model can be linearized by inverting it to give:
Thus, a plot of 1/k (y) versus 1/c2 (x) will yield a straight line with a slope of cs/kmax and an intercept of 1/kmax. The data can be set up in tabular form and the necessary sums computed as in table below.
The means can be computed as:
The slope and intercept can then be calculated with Eqs (14.15) and (14.16) as in textbook.
The least-squares fit of the transformed data is 1/k = 0.09666 + 0.20201(1/c2).
The model coefficients can then be calculated as:
kmax = 1/0.09666 = 10.34554
cs = 0.20201 x 10.34554 = 2.0899
The growth rate at c = 2 mg/L can be predicted as:
1/k = 0.09666 + 0.20201(1/4) = 0.1471625
k = 6.7952 per day
*The linregr M-file can also be used to determine the least-squares fit:
>> format long
>> c = [0.5 0.8 1.5 2.5 4];
>> k = [1.1 2.5 5.3 7.6 8.9];
>> [a,r2,syx] = linregr(1./c.^2,1./k)
a =
0.202005196520525 0.096665700618091
r2 =
0.999569288346182
syx =
0.007995513530533
The model coefficients can then be calculated as:
>> kmax = 1/a(2)
kmax =
10.344930969370603
>> cs = kmax*a(1)
cs =
2.089729813458969
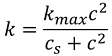






No comments:
Post a Comment